カービングターンと「推進力」
お疲れ様です。今回も「レースラフティングにおける運動エネルギー」の続きです。
ようやくですが、そろそろ、このテーマも架橋に入って来ました(笑)
「カービングターンにおける”推進力”の重要性」についての説明になります。
ここまでの流れです。
- レースラフティングにおける「運動エネルギー」
- レースラフティングにおける「運動エネルギー」 の基本原則
- ラフティングと「エネルギー保存の法則」?
- 減少する「ボートの運動エネルギー」
- 運動エネルギーが減ったら?⇒加えれば良い!
- ちょっとまとめます♪(レースラフティングにおける運動エネルギー)
- ラフティングと「慣性の法則」
- ラフティングにおいて「慣性」は敵か味方か?
- 敵にも味方にもなりえる運動エネルギー!
- 運動エネルギーの方向の変換!
- 変換させたものとは!?
- 運動エネルギーの方向変換部分で起こっていること(一例)
- 外側、そして内側からも変換!
- ラフティングのボート周辺には「水」がある♪
- ラフティングにおける『カービングターン』♪
- カーブの内側で・・ラフティングにおける「カービングターン」
- カーブの外側で・・ラフティングにおける「カービングターン」
- カービンターンの”壁”を作る♪
- 「壁」と「反作用の力」とで跳ね返すカービングターン
- カービングターンにおける「関係式」
毎度ながら・・⬇
前回は”カービングターンにおける力の関係式”というものを紹介しました。
こちらです
↓ ↓
=「ボートに対しカーブの外側に向かう力(カービング力)」
+
「ボートの真後ろ方向に受け流された力(推進力として残された力)」
この関係式が「カービングターンにおける”推進力”の重要性」と非常に大きく関わってくるのです!
今回はそのことについて説明していきます。
つまり、「ボートの推進力」というものが、「カービングターン」を実践するにあたっての、”カービングの効き目”にどのような影響を及ぼしていくか???
ということについてです。
まずこちらのイメージ図を見てください。
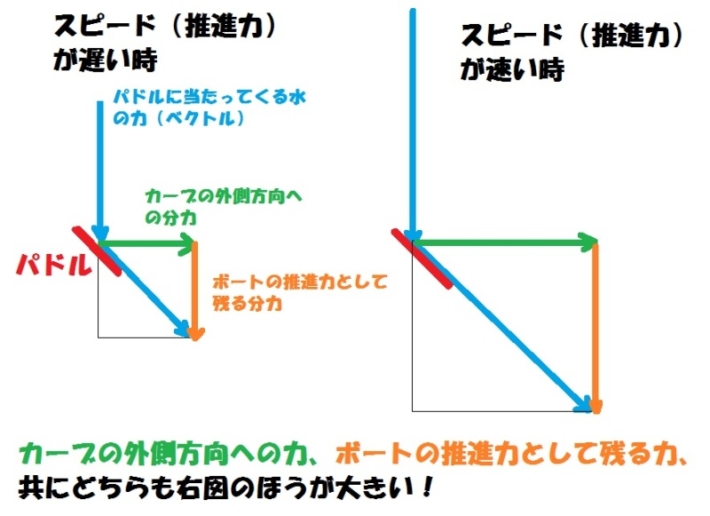
ボートのスピードが遅い時と速い時の、パドルに当たってくるときの「力(ベクトル)関係」の比較です。(あくまでもイメージです)
ベクトルとは、向きと大きさを持つ力のことです。その矢印がベクトルの向きを意味し、長さがベクトルの大きさを意味します。 →つまり「線が長いベクトル」ほど「大きい力」となります。
図の赤い線の「パドル」というのが、”反作用の力を生み出す壁”を作っているパドルです。上の図においてパドルの角度は同じものとします。
実際の画像で確認するとこれですね⬇
比較図を見てもらえれば分かるように、
ボートのスピードが速いときほど(=ボートに推進力があればあるほど)、そのパドルに向かってくる水の力は大きくなってきます。
と同時に、パドルの角度が同じであるなら、
その力の分力である「ボートに対しカーブの外側に向かう力」と「ボートの真後ろ方向に受け流された力(はね返したとも)」の2つも、それに比例して大きくなるということです。
カービングターンにおける力の関係式のところでも書いていますが、
「ボートに対しカーブの外側に向かう力」の「反作用の力」が、カービングターンをする際のボートの横滑りを防いでくれています。
つまり、これは「カービング力」とも言えるわけです。
一方「ボートの真後ろ方向に受け流された力(はね返した)」というのは、以前の記事でも書いたように「推進力として残された力」とも言えます。
ここまでは大丈夫でしょうか??
では、ここからの説明が、今回の重要な部分となってきます。
例えば、”あるカーブ”を進んでいくためには、最低限必要な「カービング力」があったとします。
横滑りをしないカービングターンをするために必要な「カービング力」の大きさ・・という意味です。
その力をいつものように”ベクトル”で表します。
ベクトルの長さは、その力の強さを表し、その向きが力の向きそのものを表します。
図で表すとこんな感じです。
つまり、カーブの外側方向に対し、最低でもこの長さのベクトルが必要というわけです。
では、次に、この最低限必要な「カービング力」を得るためには、どんな状況が必要になってくるのかを2つのパターンで示します。
①スピードが遅い=推進力が弱いパターン
②スピードが速い=推進力が強いパターン です。
イメージは次のようなものとなります。
再度確認しますが
①がスピードが遅い=推進力が弱いパターン。
②がスピードが速い=推進力が強いパターンです。
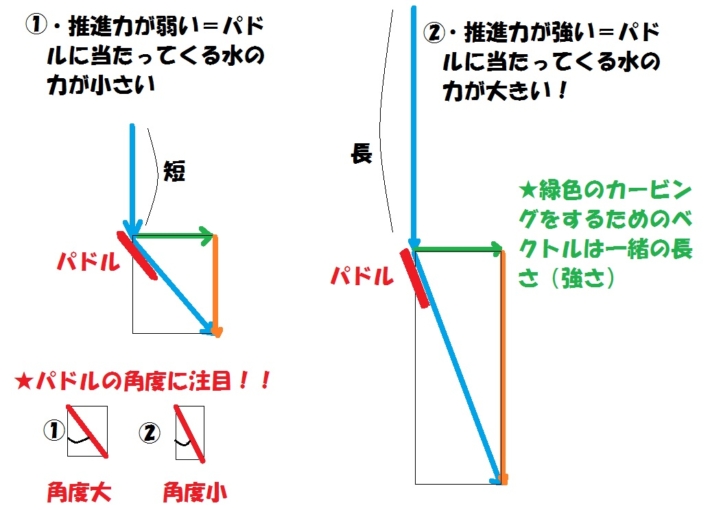
①と②を比較してよく見てみてください!
どちらも必要とされる緑色の「カービング力」の強さは一緒です(長さが同じということ)
しかし、当然スピードが違うので「パドルに当たってくる水の強さ」が違います!
これは水色のベクトルですね。
そして、それに応じて、オレンジ色の「推進力として残る力」も違ってきます。
②のほうが大きい(ベクトルの線が長いということ)ですね!
これはカービングの関係式から考えても、簡単に理解できることでしょう。
再度載せますがが、こちらの式です。
=「ボートに対しカーブの外側に向かう力(カービング力)」
+
「ボートの真後ろ方向に受け流された力(推進力として残された力)」
そして、もう一つ注目すべき「違い」があります!
それは、パドルの角度です!!
同じ「カービング力」を得るための、パドルの角度というものが、①と②で全く異なってくるのです!
スピードが遅いほうの①では、ボートの中心軸(ボートの進行方向)に対し、やや広い角度となっています。
一方、スピードが速い②では、その角度は①よりも狭くなっているのです。
この「パドルの角度」というものが、ボートスピードに大変大きな影響を与えてくるものなのです。
なぜかというと、
もし、ボートが「ボートの中心軸」と同じ方向に、真っ直ぐに進んでいると仮定するならば(ここ重要です)、
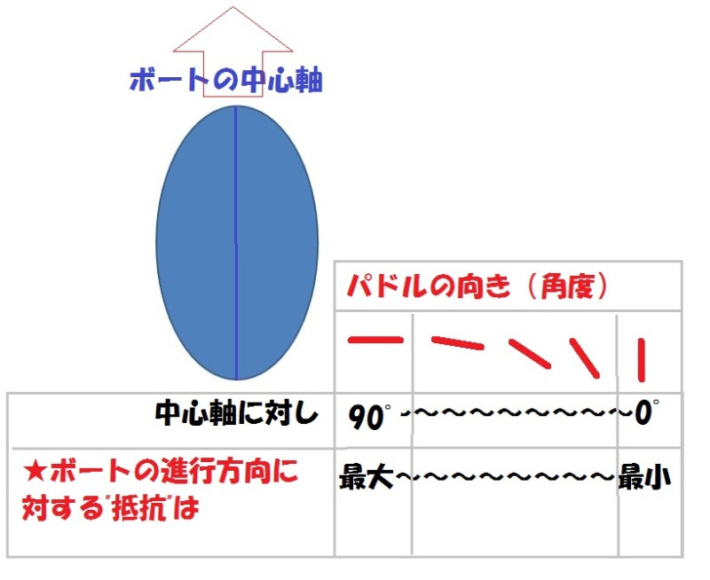
ボートの進行方向(ボートの中心軸)に対して、パドルの角度が広くなればなるほど、その「ブレーキ要素=抵抗」というものは大きくなってしまうからです。
つまり、ボートのスピードを減速させてしまうということになります。
逆に、その角度が鋭角になればなるほど、「ブレーキ要素=抵抗」が少なくなるので、スピードの減速も小さいものとなるのです。
図で表すと以下のようなものとなります。
つまり、ボートのスピードが速ければ速いほど、推進力が強ければ強いほど、より”鋭角なパドルの角度”でもって、その状況に必要な(最適な)「カービング力」を得られるということなのです。
より、”鋭角なパドルの角度”ということは、”より少ないブレーキ要素”ということです。
結果、より少ないブレーキ要素でもって、最適なカービング力を得られるということになります!
つまり!!!
ボートに推進力があればあるほど、”カービングの効き目”というものは強くなるということなのです!
これは、もちろんそれを実行できる正しい技術、チームワークがあってのことですが・・・(笑)
加えるなら、私がこのブログで載せているイメージ図というものは、あくまでも「イメージ」です。
実際の状況においては、もっともっと複雑なものとなっている場合はもちろん、このイメージ図とは若干異なるケースも少なくないはずです。
ボートの下にある「水」も、全部が同じ状態とは限りませんから。静水であっても部分的に少し流動している事もありかもしれませんし・・。
<補足情報>
より厳密に説明すれば、同じカーブを曲がっていく場合には、ボートスピードの速度の比例して、カーブの外側に向かって働く遠心力も大きくなっていきます。
つまり、カービングターンを実現する為には、より大きなカービング力が必要となってきます。
「え?じゃあ、速く進んでも結局は、それだけブレーキを大きくしなくてはいけないのでは??」
と思うかもしれませんが、ここで再度思い出してもらいたいことは、「ボートスピード(推進力)が速ければ、それだけ大きな水の力がパドルに当たってくる」という事です。
その「大きな力」を自身のパドルにおいて、「カービング力」と「推進力」に分配していくわけです。
確かに速度が速くなれば、同じカーブにおいても「より大きなカービング力」が必要になってくるのは事実ですが、それと同時に「より大きな推進力」を得ることが出来ているのです。
ようするに、この2つの力「カービング力」と「推進力」を自身のパドル操作によって、どれだけ上手い具合に分配できるかどうか?・・に、カービングターンの成否がかかってくるのです。
当然のことながら、ベストな分配具合とは『最小限度のカービング力だけ得て、残りは全て推進力に使う』になります。
しかし、感覚的なイメージとしては、すべての状況において「全く同じ原理」なのです。
実際の状況にどうれほど合わせられるか?調整できるか?が、その人・そのチームの技術の見せ所ということになるでしょう。
また次回に続きます。
そろそろまとめに入りたいと思います!














ディスカッション
コメント一覧
まだ、コメントがありません