カービングターンにおける「関係式」<レースラフティング>
引き続き「レースラフティングにおける運動エネルギー」の記事です。
今回からは「カービングターンにおける”推進力”の重要性」を書いていきます♪
ここから、さらに専門的な内容となっていきます。
ここまでもかなり専門的な記事となっているので、もはやこれらの記事を読んで頂いている方々はかなり少数となっているでしょう。
いや・・・もしかしたらいないかも・・・という心配もありますが(笑)でも、せっかくなのでもうちょっとだけ書いていきたいと思います!
ここまでの流れです。
- レースラフティングにおける「運動エネルギー」
- レースラフティングにおける「運動エネルギー」 の基本原則
- ラフティングと「エネルギー保存の法則」?
- 減少する「ボートの運動エネルギー」
- 運動エネルギーが減ったら?⇒加えれば良い!
- ちょっとまとめます♪(レースラフティングにおける運動エネルギー)
- ラフティングと「慣性の法則」
- ラフティングにおいて「慣性」は敵か味方か?
- 敵にも味方にもなりえる運動エネルギー!
- 運動エネルギーの方向の変換!
- 変換させたものとは!?
- 運動エネルギーの方向変換部分で起こっていること(一例)
- 外側、そして内側からも変換!
- ラフティングのボート周辺には「水」がある♪
- ラフティングにおける『カービングターン』♪
- カーブの内側で・・ラフティングにおける「カービングターン」
- カーブの外側で・・ラフティングにおける「カービングターン」
- カービンターンの”壁”を作る♪
- 「壁」と「反作用の力」とで跳ね返すカービングターン
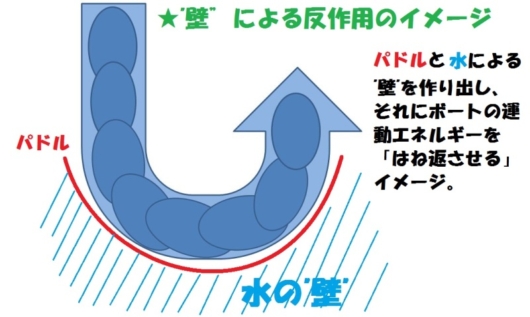
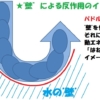
まずは、前回紹介した「水から受ける反作用の力」を利用した”壁”のイメージです。
今回説明している方法では、ボートの持っている運動エネルギーをそのまま”跳ね返す”、そのまま”利用する”という点が重要です。
ですから、ボートがカーブに進入する前までに充分なスピードをボートに持たせることが大切なのは当たり前なのですが、それに加えて、
カーブを進んでいる最中にも、ボートにスピードを与え続ける、ボートに推進力を与え続けるというのが、非常に重要なこととなってきます。
つまり、
2 カーブにおいて、ボートにさらに運動エネルギー(推進力)を与え続ける
という作業をしていくことになるわけです。
なぜなら、この「ボートの推進力」というものが、「カービングターン」を実践するにあたっての、”カービングの効き目”に大きな影響をあたえてくるためです。
”カービングの効き目”というのは、
カーブを進んで行くときに、どれだけボートが外側に横滑りしないで、進行方向に進めるのか・・・ということです。
車で言うなら、グリップ走行におけるタイヤのグリップ力になるのでしょうか??
この”カービングの効き目”を大きくすることが、上手くカービングターンをしていくのに不可欠なのは言うまでもありませんね。
では、いきます♪
まずは、最初にこの画像を確認しておきます。
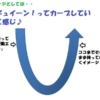
この場面では、ボートの右後ろにいる選手(私)が、水中にパドルを入れて、
・ボートの運動エネルギーの方向の変換(他の選手も行なっていますが、メインは私)
・ボートのカーブ外側への横滑り(スライド)を防ぐ
ということを行なっています。
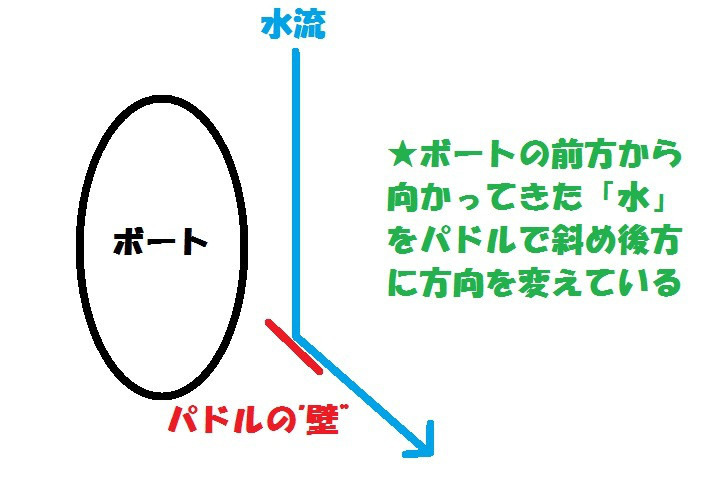
これは、ボートの前方から流れてくる(近づいてくる)水を、自らのパドルに当ててて、そのような効果を生み出しているのです。
(この辺は前回の記事です)
このときの状況はこんな感じです。
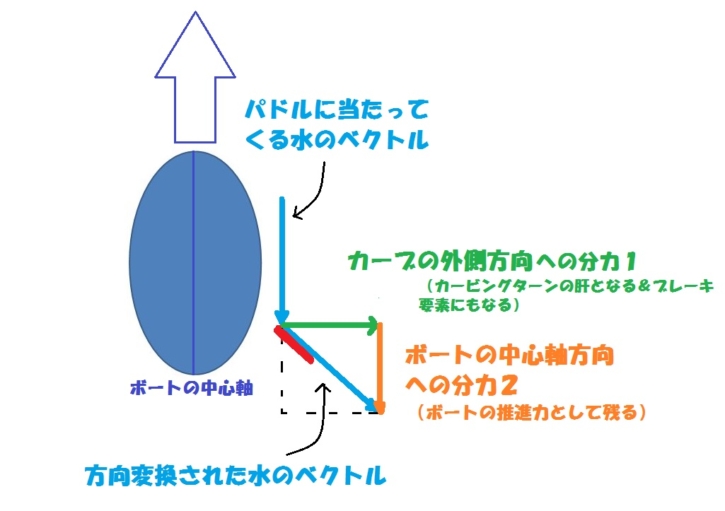
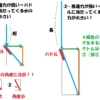
では、この「方向変換された水の力」というものをボートの中心軸に対し、垂直方向と平行方向の「2つの力」に分解します。
「力の分解」とは、「力の合成」の逆ですね。
ちなみに「力の合成」については、こちらの記事で簡単な説明をしています。
つまり、「方向変換された水の力(ベクトル)」を対角線とする平行四辺形の2辺が分力となります。
分解された「2つの力」とは、
1 カーブの外側方向への分力
2 ボートの中心軸と同方向への分力
です。
その時のイメージはこちらです。
この2の「ボートの中心軸と同方向への分力」というのは、ボートの「ボートの真後ろ方向に受け流された力(はね返したとも)」とも言えます。
つまり、
パドルに当たってきた水の力を、
②ボートの真後ろ方向に受け流された力(はね返したとも)
の「2つに分けた」・・・と言い換えることもできます。
「2つに分けた」という表現は、本当に力を2方向に分けたわけではありません。実際に目で確認できるものではありませんからね(^O^)
ここで紹介しているカービングターンの「力学的な理屈」を視覚的に理解しやすいように、このように説明しています。
パドルに当たってきた力(運動エネルギー)を弾き返した時の力を、「あえて2つの方向に分解すると、こうなる」と思ってもらえらば良いです。
<⬇上と同じ図>
「カーブの外側方向への分力」(図の緑色)は、その「反作用の力」により
ボートのカーブ外側への横滑り(スライド)を防ぐ力
(=カービングの効き目)
と言い換えることができます。
<⬇上と同じ図>
そして「ボートの真後ろ方向に受け流された力(はね返したとも)」(図の茶色)は、言い方を変えれば、
ボートに何のブレーキ要素も与えることなく真後ろに受け流された力
とも言えるわけです!
つまり、ボートの推進力によって生まれた力を、そのまま「受け流した」ということになるので、これはまた別の言い方をすれば
「推進力として残された力」 とも言えるでしょう!
<補足説明>
この記事では、「ボートの真後ろ方向に受け流された力(はね返したとも)」として、同じ力を
・ボートの真後ろ方向に受け流された力
・ボートの真後ろ方向にはね返した力
と2つの言い方を併記して使っています。一見、矛盾している表現にも感じられるかもしれませんが、結局は同じことを意味しています。
「角度を付けたパドルに水からの力を受ける」という物理的現象を、ある人は「受け流す」と感じたり、またある人は「はね返す」と感じたりもするでしょう。
ここはその人の主観・感じ方にもよります。
「はね返す」と表現した場合には、その「はね返した力」には作用反作用の法則により、ボートを前に押し返す力が働きます。
この「ボートを前に押し返す力」と、上で説明している「「推進力として残された力」は全く同じ大きさの力(運動エネルギー)です。
なので、結局は同じことなのです・・・
ややこしくてすみませんm(__)m
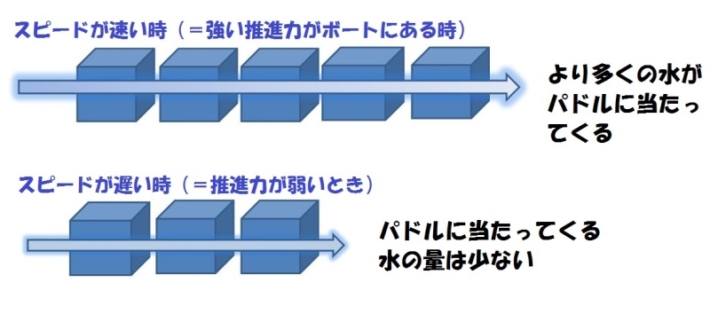
ちなみに、「パドルに当たってくる水の力」というものは、ボートが前に進む速度が速ければ、速いほど大きくなります!
なぜかというと、ボートの進行方向(直線やカーブでも)に進む速さが速いほど、より「多くの水」がパドルに当たってくるからです!
より多くの水の量が当たってくるので、その力も大きくなるのは当たり前ですね♪
つまり、この「パドルに当たってきた水の力」というものはボートの持つスピード(それを生み出す推進力)が速ければ速いほど大きくなるということです。
なんだか、かなり「ややこしく」なってしまいました・・・・
これらの関係をまとめて式に表すと、次のような「関係式」になります!
=「ボートに対しカーブの外側に向かう力(カービング力)」
+
「ボートの真後ろ方向に受け流された力(推進力として残された力)」
この関係式が「カービングターンにおける”推進力”の重要性」と非常に大きく関わってくるのです!
長くなってきたので今回はここまで。













ディスカッション
コメント一覧
まだ、コメントがありません