運動エネルギーの方向変換部分で起こっていること（一例）
さてさて、今回も「レースラフティングにおける運動エネルギー」の記事です。
ラフティング競技において、ボートを操作する上で非常に重要となってくる「慣性の取り扱い」について説明しています。
（2007年韓国での世界大会。オーストラリアチームにて）
ここまでの流れです。
- レースラフティングにおける「運動エネルギー」
- レースラフティングにおける「運動エネルギー」 の基本原則
- ラフティングと「エネルギー保存の法則」?
- 減少する「ボートの運動エネルギー」
- 運動エネルギーが減ったら？⇒加えれば良い！
- ちょっとまとめます♪（レースラフティングにおける運動エネルギー）
- ラフティングと「慣性の法則」
- ラフティングにおいて「慣性」は敵か味方か？
- 敵にも味方にもなりえる運動エネルギー！
- 運動エネルギーの方向の変換!
- 変換させたものとは！？
前回の続きです。
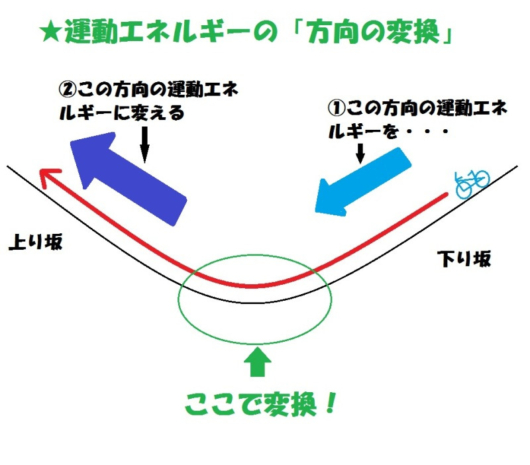
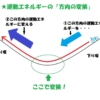
「自転車で、坂道を下って、そして再び上がる」という状況を例にし、「運動エネルギーの方向の変換」が起こっているケースを紹介しました。
その時のイメージとしてはこんな感じです。
図で見てもらえれば分かるように、この時の自転車の運動エネルギーの向きは、「左斜め下向き」から「左斜め上向き」へと変わっています。
では、今回は、この時の「運動エネルギーの方向の変換」がどのように起こっているかを考えて行きたいと思います。
（なかなかラフティングにいきませんが、ちゃんとあとで繋がっていきます♪）
まず、この「運動エネルギーの方向の変換」が起こっている部分に焦点を当てていきたいと思います。
つまり、道路が「下り坂」から「上り坂」に変わっている部分です。
上のイメージ図でいうと緑で囲った円形のところですね。
この緑の円形内の道路の曲線の部分です。
ここの最下部を拡大していきます。
さらに拡大していきます・・・・（頭の中で）
さらに、もっともっと拡大していきます・・・・・（頭の中で）
もっと・・・もっと・・・
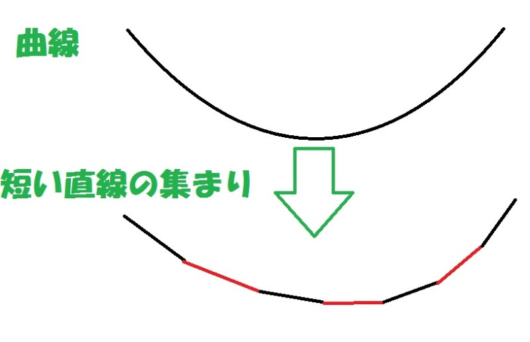
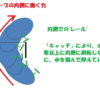
すると、この曲線部分の最下部は、最終的に、”ものすごく短い直線部分”になると考えることが出来ます。
ようするに、ゆるやかな曲線を、
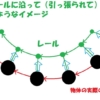
「数多くの、ものすごく短い直線が、少しづつ角度を付けて、連なっているもの」と考えてみてください。
イメージは、こんな感じです。
これはかなり大雑把なイメージですが・・・・
すると、この曲線の最下部では、自転車の運動エネルギーは、こんな感じでその方向を変換したと考えることができます。
↓ ↓ ↓
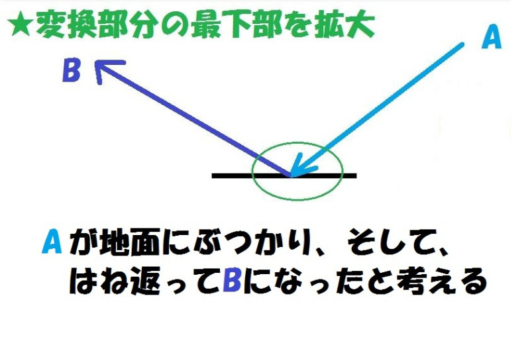
Aという運動エネルギーが、下り坂を下ってきた自転車の運動エネルギーです。
そして、Bという運動エネルギーが、登り坂を上がっていく自転車の運動エネルギーです。
ここまで、大丈夫でしょうか？
では、ここから、どのようにしてAという運動エネルギーが、Bという方向の異なる運動エネルギーに変わっていったのかを、簡単に説明します。
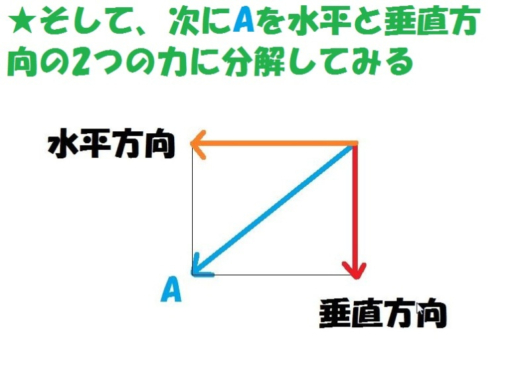
まず、このAという運動エネルギーを、2つの力に分解します。
”水平方向の力”と”垂直方向”の２つの力です。
「力の分解」とは、「力の合成」の逆です。
「力の合成」については、こちらの記事で簡単な説明をしています。
つまり、”Aという力”を対角線とし、さらに、水平方向と垂直方向に2辺を持つ平行四辺形（実際には長方形となる）をつくるわけです！
この時の2辺の長さが、そのまま其々の力の大きさとなります。
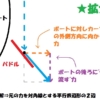
このときのイメージはこちら
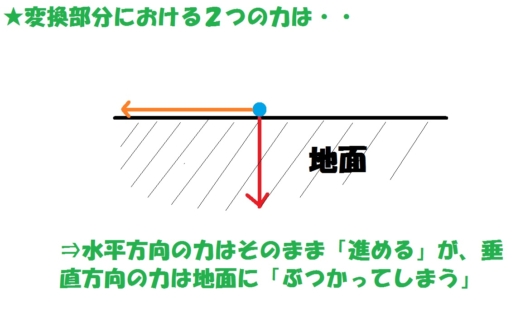
つまり、Aという力は、上の図でいえば、オレンジ色（水平方向）と赤色（垂直方向）の2つの力の合力というわけです。
では、この２つの力が、先ほどの「運動エネルギーの方向の変換」が起こっている曲線の最下部（短い直線）ではどうなっているのかというと・・・・・
こうなっています！
↓ ↓ ↓
水平方向の力は、そのままの方向で進みます。
これは当たり前ですね。その方向には何もありませんから、当然、そのまま進み続けます！（これも慣性の法則です）
しかし、垂直方向の力はそうはいきません。
すぐ下に地面があるので、当然、地面にぶつかります！！
するとどうなるでしょうか？？
ぶつかったら、跳ね返るのです！！
これは、「作用反作用の法則」というものですね♪
「作用反作用の法則」とは、
ある物体が他の物体に力（作用）を及ぼすとき、それとは逆向きで大きさの等しい力（反作用）が常に働く
というものです。
つまり、こうなります。
↓ ↓ ↓
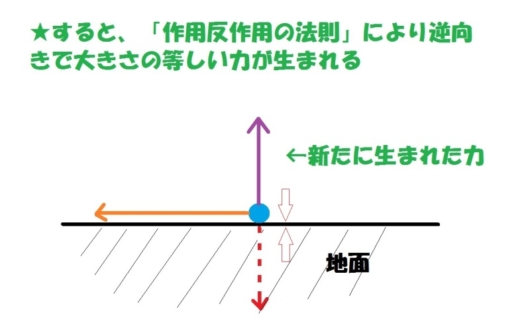
地面にぶつかった力は、この法則により、その逆の方向（地面から上に垂直にあがる方向）に、等しい大きさで、新たに生まれ変わるというわけです。
図でいうと、紫色の力ですね。
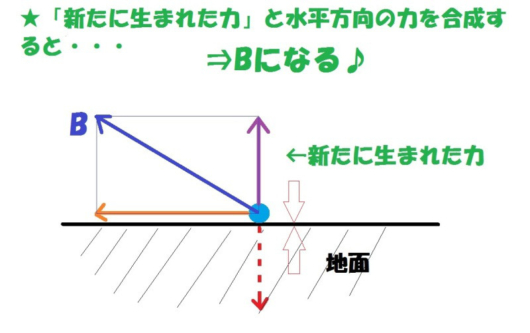
そして、この新たに生まれた「紫の色の力」と、もともとあった「水平方向の力」を合成させると・・・・・
こうなります！
↓ ↓ ↓
Bになりました♪
最初の図に戻りましたね（笑）
つまり、Aという力は、地面にぶつかった際に、地面からうける「作用反作用の法則」により、Bという力に生まれ変わったのです！！
これが、このケースにおける運動エネルギーの方向の変換となっているわけです！！
今回、説明した内容は、レースラフティングにおける「カービングターン」の原理に大きく影響してくる内容です。
だいぶ長くなったので、また次回に続きます